商品簡介
※試閱動畫※
在數學教學中,引導學生認識證明,是進入數學性思考,很扎實的一環。一般教科書大都採用文字敘述、符號表達、邏輯推演,嚴謹地向學生呈現直接、間接證明法和數學歸納法。但作者在教學過程中,觀察到學生有多元的學習能力,透過眼到、心到、手到等方式,找到屬於自己學習的方式。這不僅是靠運算式的堆疊,也需要繪製適當圖形作為輔助,更需懂得結合「數」與「形」之間的關係,相輔相成之下,才能獲得最大的學習效益,於是作者將多年的教學經驗與發現,匯整出此書與讀者大眾分享。
【簡單易懂的幾何圖像解釋】
讓原本枯燥乏味的文字證明轉變為幾何圖像清楚呈現!
【配合高中職教學內容】
清楚標示證明所對應的定理、公式,讓學生了解不同於課本上的解釋方法,並能有效利用圖像加深印象。
作者簡介
1983年出生於臺南,畢業於國立臺灣大學,現任於新北市立新北高級中學(原國立三重高中)。致力於中學數學教育,在教育現場得知許多人在學習數學時,或多或少有過挫敗感,對數學理論存在距離感。喜歡揉合科普知識及正規教材,用簡單有趣的方法教學,期望以淺顯易懂的方式,與學生、讀者分享多元化的數學觀。
名人/編輯推薦
◆師大數學系退休教授 洪萬生教授◆
在數學書籍中,插圖(graphical illustration)一向不可或缺,因為它們有助於我們對於相關數學知識的理解。不過,在古希臘時代,哲學家柏拉圖卻認為它應該只是數學學習的輔助工具,而非主體。現在的數學書籍(無論是教科書或普及書籍)也非常重視插圖,不過,它們混跡於數學知識內容之中,多半還是居於客卿的角色,儘管所有的作者都不在乎柏拉圖的工具說之意義何在。
現在,無論是《無字證明》或是《按圖索驥》,插圖都被推到數學普及最前線,它們不再是配角,而是成了主角。因此,教師如何運用插圖本身,讓它們自行「說故事」,以掌握或促進數學學習的成效,是我們必須面對的嚴肅議題。以本書為例,作者將圖形適當拆解,並穿插相應的公式,充分反映了「圖說一體」的特色,值得我們細細咀嚼與品味。
◆師大數學系 許志農教授◆
一張好的圖勝過繁雜的推理過程!
蔡宗佑老師用心整理,蒐集與歸類中文版的無字證明,除了講究圖形的美觀與一致性外,也著重用精簡的文字來闡釋數學公式或定理。相信這些範例足以提供老師與學生們活用與欣賞。這本中文版的無字證明書籍的出版也可以拋磚引玉,讓國人在這方面有更豐富的資訊,特此推薦。
◆建中名師 林信安老師◆
《按圖索驥──無字的證明2》與一般的數學讀物很不同,沒有長篇大論與滿滿的數學式子。作者企圖透過一系列的圖形帶領讀者去揭開數學公式與定理之謎。除了詳細解說圖形的關係外,也巧妙運用色彩呈現出定理與公式的推導,使得圖形更能發揮詮釋數學定理與公式的證明。
教學現場中適當利用圖形呈現,會使得初學者產生熟悉而自然的感覺,閱讀《按圖索驥──無字的證明2》會給讀者「一張圖勝過千言萬語」的效果,這就是我想推薦這本書的理由!
序
萊茵巴哈(H.Reichenbach)曾將科學的學習歷程分為:發現及驗證(the context of discovery and the context of justification)兩個階段。人類不斷地透過觀察自然,體察事物,利用邏輯找出及發現可能的模式,再敘述及驗證之,達到分析、體認這自然世界,來說明、闡述自然哲理,更能運用這模式與能力做抽象思考以及解決所遇到的問題。
敝人感謝三民書局,特別是臺灣大學的蔡聰明教授,指導及幫忙審定,並給了我這個機會向數學界,特別是國、高中生及奉獻給中學教育的前輩、老師們呈現這本作品,這是屬於是理解數學證明的小品。在從事數學教學中,引導學生認識證明是進入數學思考中很扎實的一環,介紹:直接證法、間接證法和數學歸納法,利用文字敘述、符號表達、邏輯推演都盡可能嚴謹地向學生呈現。敝人觀察出學生有多元的學習能力,透過眼到、心到、手到等等方式,找到屬於自己學習數學的竅門,不獨是運算式的堆疊,也需要繪製適當圖形作為輔助,更是數與形兩大數學學理根基的展現,於是在教學歷程累積下來,整理出這一本「按圖索驥」!
目次
推薦序一
推薦序二
C4三角學
4-01 平方關係
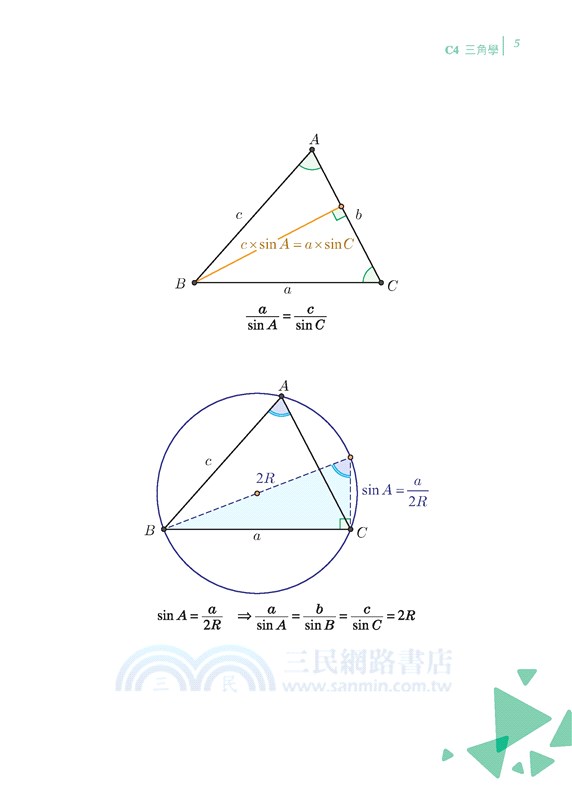
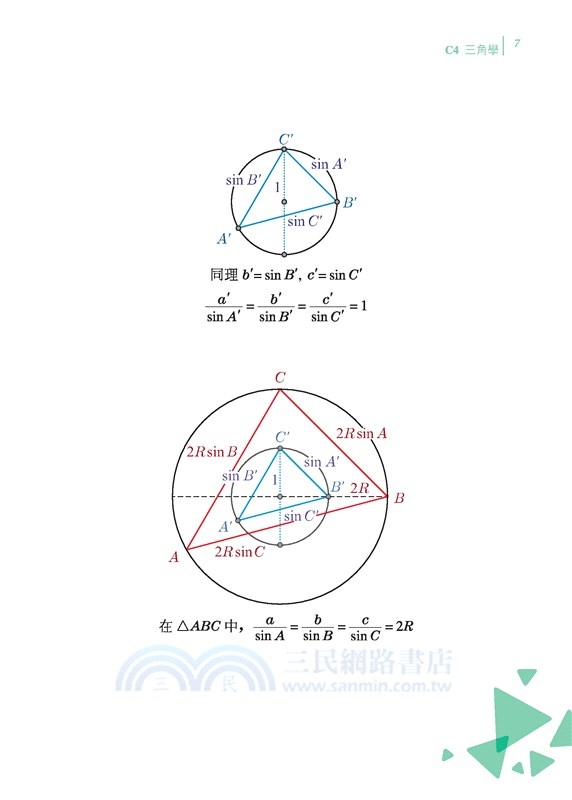
4-02 正弦定律(Law of Sine)
4-03 正弦定律(Law of Sine)
4-04 餘弦定律(Law of Cosine)
4-05 餘弦定律(Law of Cosine)
4-06 畢氏定理(另證)
4-07 餘弦定律(Law of Cosine)
4-08 由托勒密定理推導餘弦定律
4-09 正餘弦定律之複數證法
4-10 正弦和角公式
4-11 正弦和角公式
4-12 餘弦和角公式
4-13 正弦差角公式
4-14 正弦和角公式
4-15 正弦和角公式
4-16 正餘弦和角公式
4-17 正餘弦差角公式
4-18 正切和角公式
4-19 正切差角公式
4-20 正切差角公式
4-21 正切差角公式
4-22 正弦二倍角公式
4-23 餘弦二倍角公式
4-24 正餘弦二倍角公式
4-25 正切半角公式
4-26 以正切值表達二倍角公式
4-27 正切三倍角公式
4-28 正弦疊合
4-29 正弦疊合
4-30 和化積公式
4-31 和化積公式
4-32 差化積公式
4-33 差化積公式
4-34 海龍公式
4-35 已知三中線長度之三角形面積
4-36 tan^(-1)(1/2)+tan^(-1)(1/3)=(π/4)
4-37 tan^(-1)1+tan^(-1)2+tan^(-1)3=π
C5數列與級數
5-01 連續整數和
5-02 連續整數和
5-03 連續整數和
5-04 連續奇數和
5-05 連續奇數和
5-06 1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n^2
5-07 1+3+…+(2n-1)+(2n+1)+(2n-1)+…+3+1=n^2+(n+1)^2
5-08 連續平方和
5-09 連續平方和
5-10 連續立方和
5-11 連續立方和
5-12 連續立方和
5-13 連續立方和
5-14 連續立方和
5-15 連續平方和
5-16 連續四次方和
5-17 Σ(-1)^(k+1)k^2=1^2-2^2+3^2-4^2+…+(-1)^(n+1)n^2=(-1)^(n+1)*n(n+1)/2
5-18 n^2-(n-1)^2+…+(-1)^(n+1)1^2=n(n+1)/2
5-19 費氏數的平方和
5-20 費氏等式(Ⅰ)
5-21 費氏等式(Ⅱ)
5-22 費氏等式(Ⅲ)
5-23 費氏等式(Ⅳ)
5-24 連續三角數的和
5-25 連續三角數的和
5-26 連續三角數的和
5-27 交錯三角數級數
5-28 兩相連整數乘積的和
5-29 三相連整數乘積的和
5-30 三角數等式
5-31 兩相鄰三角數的平方和
5-32 兩相連三角數的和
5-33 三角數等式
5-34 三角數等式
5-35 奇數平方可表示成8倍的三角數加1
5-36 奇數平方可表示成兩三角數的差
5-37 組合等式
5-38 惠更斯級數
5-39 n層的a邊形數
C6極限與微積分
6-01 歐拉數e的定義
6-02 lim(x/e^x)=0
6-03 幾何迭代法求極限值
6-04 無窮等比級數
6-05 無窮等比級數
6-06 無窮等比級數
6-07 無窮等比級數
6-08 無窮等比級數
6-09 無窮等比級數
6-10 無窮等比級數
6-11 無窮等比級數
6-12 交錯級數
6-13 1*1+2*1/2+3*1/4+4*1/8+5*1/16+…=4
6-14 積分和等於1
6-15 分部積分法
主題書展
更多書展今日66折
您曾經瀏覽過的商品
購物須知
為了保護您的權益,「三民網路書店」提供會員七日商品鑑賞期(收到商品為起始日)。
若要辦理退貨,請在商品鑑賞期內寄回,且商品必須是全新狀態與完整包裝(商品、附件、發票、隨貨贈品等)否則恕不接受退貨。