商品簡介
微積分如何誕生?
微積分是什麼?
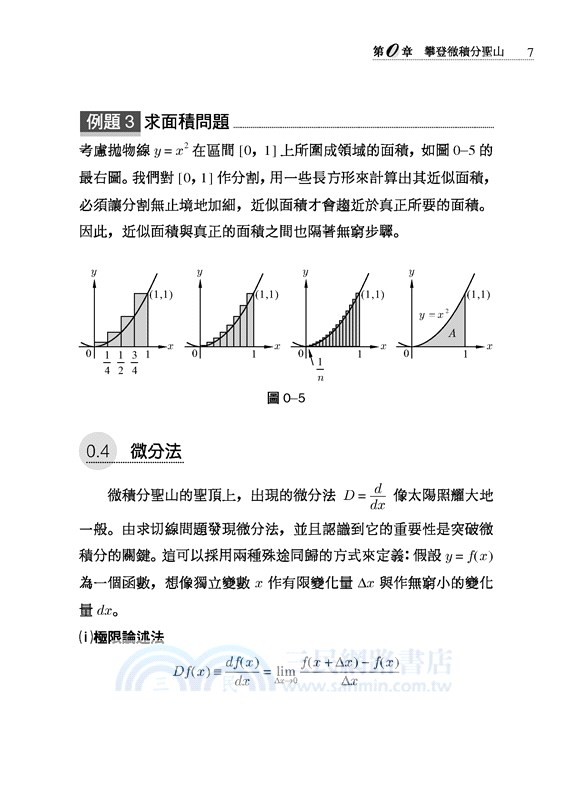
微積分研究兩類問題:求切線與求面積,分別發展出微分學與積分學。
微積分最迷人的特色是涉及無窮步驟,落實於無窮小的演算與極限操作,
所以極具深度、難度與美。
從古希臘開始,數學家經過兩千年的奮鬥,累積許多人的成果,到了十七世紀,
終於由牛頓與萊布尼茲發展出微分法並且看出微分與積分的互逆性,
從而揭開求切、求積、求極、變化與運動現象之謎,於是微積分誕生。
講述這段驚心動魄的思想探險之旅,就構成了本書的主題。
作者簡介
蔡聰明
已從臺大數學系退休。目前過著耕讀的生活,隨興旅遊兼從事寫作。
對於數學教育與普及數學的工作難以忘情
夢想者:從音樂中看出數學,並且從數學中聽出音樂
名人/編輯推薦
行走在文化脈絡裡
如果從埃及紙草上記載的實用算術問題算起,數學的歷史至少也有三千五百年之久。雖然經歷了這麼漫長的歲月,它卻保持住一種迥異於其他學科的特色,就是每項 數學命題一經證實,就永遠不會被推翻。當然敘述真理的方式有可能修正,理解觀念的角度與深度也有可能變遷。譬如,「什麼是數」這個問題,今人與古人的認識 就大有差距。然而,「質數有無窮多」的命題,一經古希臘人證明,迄今以至未來都不會動搖。
現在大學一年級教的微積分內容,基本上在18世紀就已經完備。然而多數教科書是按照「邏輯的脈絡」來書寫,奠基在19世紀Weierstrass從實數系統出發,而以e-d符號作表述的鋪陳法。根據嚴謹邏輯進程寫出來的教科書,雖然內容精鍊,觀念明晰,但是往往不容易讓初學者掌握想法因何而生,內容為何如此展開,要解決的問題的重要性又在哪裡。也就是說,學習者的認知歷程,常常與知識的邏輯架構發生扞格。
要協助學習者克服上述的障礙,同樣的課程內容,需要放在「文化的脈絡」裡重新檢視。這個脈絡又可分為外在與內在兩個面向:外在是指發展微積分的歷史與社會 背景,從此可觀察微積分核心問題為何以及如何被提出;內在是指數學理論體系本身的辯證發展,從此可看出舊瓶如何不斷裝進新酒,概念的內涵如何持續豐富化。
歷年來,世界各國不知出版了多少微積分教科書,但是永遠好像有一本更理想的仍待書寫。這種現象的產生,也許或多或少反映了「邏輯脈絡」與「文化脈絡」宛如 油與水的關係,極難均勻而穩定地交融。以臺灣微積分教學的實際環境衡量,大學生也迫切需要補充依循「文化脈絡」提煉出的營養品。
蔡聰明教授的《微積分的歷史步道》,正好及時紓解了這方面的渴求。
聰明兄是認真、踏實又謙虛的數學教授,也是我尊敬的好學之士。多年來他為普及數學知識著述不輟,選題獨到講解清楚,並且反映出廣博的文化素養。中央研究院 數學所每年暑期選擇適當專題開設研習班,協助大學生跨越平日制式的教學內容,動手動腦演練電腦技藝、研究問題、或探索學術的演化軌跡。2007年起由我負 責設計課程並延請教席,我馬上想到如果由教學經驗豐富的聰明兄,來引領學生仰視微積分發展的燦爛星空,學生將會多麼有幸地學得辨識銀河北斗。
聰明兄在溽暑之中,連續兩年鼎力支持研習計畫,現在又把講述內容著述成書,使更多的學子得以分享他的心血結晶,令我衷心感激。讀者邁步於此「歷史步道」 時,應該會感受到「有窮」與「無窮」的對峙張力。當數學家最終從「有涯」躋身「無涯」時,也應該會抒發出了悟的讚嘆。
聰明兄的大著受篇幅所限,才演義了微積分歷史的上半段,而以「微積分的根本定理」為最高潮。這個根本定理的式子,雖然只用了不多的符號,但是卻蘊含了自古 希臘迄牛頓與萊布尼茲近兩千年的思想精華。如此人類心智的結晶,自然放射出鑽石般光芒。讓我們拭目以待,聰明兄來日為微積分發展的近代歷程琢磨另一顆晶 鑽。
序
追隨大師的腳步
這一本書是為了學習微積分的人而寫的微積分發展史,適合初學者的研讀。當然讀過微積分的人,讀本書應該也是不錯的選擇。目前存在的微積分發展史的文獻,幾乎都是為數學史家寫的,不見得適合學生的研讀。
我在臺大具有三十多年的微積分教學經驗,並且也開過「微積分與西方文明」這門通識課,接觸到各學院各學系的學生,深知微積分是許多大一學生或初學者甚感困難與畏懼的科目。從一般微積分教科書無法得到幫助,因為它們通常都是逆著歷史發展的順序來書寫,並且只呈現完成後整理得嚴謹的演繹式微積分,缺乏微積分的探索發現過程。
因此,如何幫忙初學者平順地學習微積分,變成教學上的一個重要課題,這也是撰寫本書首要的考量。解決這個困難之道就是,透過微積分的發展史來呈現微積分的探索發現過程。長久以來,我對微積分史就深為喜愛,每年上微積分課,都先講述約10小時的微積分發展簡史,讓學生知道牛頓與萊布尼茲如何發明微積分,然後才進入教科書的主題。雖然是簡史,但是深受學生的喜愛。
恰好我遇到中央研究院數學研究所的李國偉教授,兩次(2007與2008年的暑假)邀請我參與中研院暑期數學營(Summer School),帶領大學部的學生探索微積分的發展史。每次為期六個星期。這個經驗對我而言,是寶貴的並且受惠良多。我要特別感謝李教授的鼓勵,甚至心中悄悄地產生要把它寫成一本書的念頭。因此,這本書可說是他催生的,特記此因緣。中央研究院數學所的環境優雅,圖書與雜誌的資料又相當豐富,那是學習與研究的樂園,這真是一個愉快並且美好的經驗!
從時間的尺度來看,微積分的發展源遠流久:從西元前六世紀,古希臘人開始遇到「無窮與連續」,到了十七世紀牛頓(Newton)與萊布尼茲(Leibniz)初創微積分,再經過兩百年的拓展與應用,到十九世紀(1880年代)才奠定邏輯基礎。微積分的成長大約花了2500年才真正大功告成。
從方法論與內容來看:微積分是透過無窮步驟的分析法,產生詭譎而難纏的無窮小量,然後再用綜合法將無窮多的無窮小量作累積;其中的微分法是微積分的核心,它的正算可以求切線,並且逆算可以求面積。詳言之,考慮兩個函數:
y=F(x), u=f(x), xÎ[a, b].
讓獨立變數x變化「無窮小量」dx,從而導致應變數y也變化「無窮小量」dy:
dyºdF(x)ºF(x+dx)-F(x)
以及無窮小的面積f(x)dx。那麼兩個無窮小量的比值與無窮多個無窮小的面積f(x)dx之連續累積,分別就是微分操作與積分操作。自然就有了兩個完美的積分公式。如何有效地求算積分?仔細作觀察與比較,靈光一閃:
如果f(x)dx可以表成dF(x)之形,亦即如果f(x)dx=dF(x)或 =f(x)或DF(x)ºF¢(x)=f(x)。因此,透過微分的逆運算,就解決了千古的積分難題。把這些概念與公式的歷史發展述說清楚,就構成了本書的內容:
| 無窮小量dx 一念噴出 乾坤震動 探尋兩千年 微積分誕生 大自然的無字天書 運動與變化的謎底 突然清晰揭開 在陽光底下 閃閃發亮 |
微積分在數學中所扮演的角色至少有三樣:它是基礎數學的總結,也是解讀「自然之書」(Book of Nature)的最佳工具,更是進入現代數學之門。微積分的誕生讓我們深刻體會,大自然是數學發展的不竭泉源,不但提供素材與問題,而且又啟示概念與方法。
本書只寫到牛頓與萊布尼茲創立微積分為止,再寫下去就會變成羅素所說的「大書是大罪惡」(A big book is a big evil.)。本書期望能夠帶領讀者追隨大師的腳步:不只是學到數學的內容,也學到數學的思考與方法。
最後要感謝楊維哲教授平時的討論,幫忙我對於數學的洞察與了悟;李國偉教授為本書寫序並且提出指正,增添本書的內涵;還有李有豐與蔡仁惠兩位教授閱讀本書所提出的許多修正意見。這些都成了本書最珍貴的資產。
目次
推薦序(李國偉教授)
自序
人名、年代與常用記號
第0章 攀登微積分聖山
第1章 畢氏學派發現「無窮」
第2章 從「有涯」飛躍到「無涯」之路
第3章 阿基米德的巧思妙想
第4章 求積方法的演進
第5章 求切線方法的演進
第6章 費瑪叩敲了微積分的大門
第7章 運動現象的研究
第8章 托里切利對微積分的驚鴻一瞥
第9章 巴羅看見了微積分學根本定理
第10章 牛頓如何發現微積分?
第11章 萊布尼茲如何發現微積分?
第12章 微分三角形的魅力
第13章 圖解微積分學根本定理
第14章 牛頓的定命性原理
第15章 抓住飛逝的瞬間
第16章 跟無窮的相遇與相知
評論 新增評論
主題書展
更多書展今日66折
您曾經瀏覽過的商品
購物須知
為了保護您的權益,「三民網路書店」提供會員七日商品鑑賞期(收到商品為起始日)。
若要辦理退貨,請在商品鑑賞期內寄回,且商品必須是全新狀態與完整包裝(商品、附件、發票、隨貨贈品等)否則恕不接受退貨。