商品簡介
本書共有四篇:
第一篇
利用具體的摺紙實作,提醒讀者像摺紙這樣的日常遊藝活動,也可以 成為正規的數學知識活動,而摺紙亦為我們作了最好的見證。
第二篇
將摺紙活動轉化為數學課堂活動,聚焦在尺規作圖以及國中基測考題。 讓讀者了解到摺紙活動所底蘊的對稱性,是數學學習所必須永遠掌握的原理。
第三篇
從歐幾里得《幾何原本》出發,介紹正 3 、 4 、 5 、 6 和 15 邊形的尺規作圖,且強調這些命題的結構地位與嚴密推理的息息相關。
第四篇
對比摺紙直觀的精確嚴密數學之必要,並總結本書的重要題旨,最後, 再將摺紙總結到現代數學的研究主題。
作者簡介
[主編]
洪萬生
臺師大數學系退休教授。專長為數學(社會)史及其與數學教育之關連,並發展成為數學普及創作、書寫與編著出版的資源和動能。自從 1998 年 10 月以來,每年發行十期《 HPM 通訊》,推動數學史與數學教學關連( HPM )的相關研究與教學。目前擔任臺灣數學博物館的策展人,利用網路虛擬環境,充實與數學知識活動有關的學習資源。
[編著]
謝豐瑞
臺師大數學系副教授。是國內將漫畫、大量操作活動編入國中數學課本的創始者,目前受聘於美國州長協會,擔任「州共同核心數學課程綱要」的審查委員。
蘇惠玉
臺師大數學系碩士,現任臺北市立西松高中數學科教師,及《 HPM 通訊》主編。研究所時主修數學史,希望以更有效的方式將數學史的材料融入數學教學中。
彭良禎
原名君智,臺師數學系碩士,現任國立師大附中數學科教師。 2007 年完成臺師大教學碩士班論文。 2000 年起在《發現月刊》發表 魔數 Math-Magics 專欄,介紹生活中精彩的多面體;現以藝數家玩摺紙專欄分享摺紙 與數學的教學經驗。
葉吉海
臺師大數學系碩士。現任國立陽明高中數學科教師。喜歡在課堂上將數學史有趣的面向與教材結合,將數學內涵與美術技巧結合,讓學生更喜愛高中數學。希望激盪出更多的藝術火花。
譚克平
臺師大科學教育研究所副教授。從事數學教育、統計教育、研究方法及評量等方面的研究。
陳宥良
臺師大科學教育研究所碩士。現任臺北市國中數學教師。教書之餘,身影常出沒於球場及書堆之中。
黃俊瑋
臺師大數學系博士生。熱愛棒球與田徑,志於數學史與數學教育之研究與學習,期望藉由數學史的融入、數學閱讀的推廣以及多元化的數學學習,讓更多人愛上數學之美。
謝佳叡
臺師大數學系博士。現任臺師大數學系助教。主修數學教育,近來積極參與國際數學師資培育研究。生性喜歡閱讀稀奇古怪的書籍,對任何事物都保有興趣,好於不疑處中有疑。近來對於古典音樂、繪畫、偵探小說有特別偏好。
劉柏宏
勤益科大博雅通識教育中心教授。研究方向為融合數學史於數學教學 (HPM) 與高等數學思考 (Advanced Mathematical Thinking, AMT ) 。 偶像是達文西,喜歡接觸任何與數學相關的跨領域知識。對於任何可以提昇學生或社會人士數學與科學素養的課程或活動都很有興趣。
趙君培
臺師大科學教育研究所碩士。現任臺北市國中數學教師。喜歡看書、運動。
名人/編輯推薦
本書一開始豐富的摺紙藝術讓數學從生活中出發,第一篇中許願星、平安符的摺法除了增添了本書的活潑性,也告訴了我們像這樣的生活常見的小東西,也涵蓋了許多數學的知識在裡頭。第二篇探討摺紙的教學概念,進而討論及國中幾何的教學,最後還介紹了國中基測中有關於摺紙與尺規的考題,再再顯示了摺紙活動所運用的原理,在數學領域中占有了一席之地。第三、四篇回歸到了數學證明的層面,將摺紙或尺規作圖所運用的理論利用嚴謹的數學來證明。也提及了為何七邊形無法用尺規作圖,有興趣的讀者不妨自我挑戰看看!
序
本文集絕大份文章都出自臺灣數學博物館所舉辦的「摺紙學數學」工作坊。而這,當然也積極呼應了我們對「數學遊戲」的一貫興趣與關懷。不過,本書之編輯,卻見證了國際數學社群與國內藝術社群的兩件事:在數學研究這一方面,摺紙數學已經逐漸受到數學界的重視,譬如 “Origami and Partial Differential Equations”(〈摺紙與偏微分方程〉,2010年5月出版)這樣的論文,會出現在美國數學學會刊物 Notices of the AMS 上,就非常令人驚奇。另一方面,國內各教育大學最近重新定位美勞教育,強調視覺藝術或造形設計人才的培育,而不再只是著眼於國小相關美勞師資之培育。我們有幸「風雲際會」,此時將有關摺紙的一些實作與論述,集結成為本書,用以彰顯此一數學遊藝的認知趣味與意義,或許也不只是巧合而已。
因此,本書除了彭良禎老師的摺紙實作經驗分享(第一篇)之外,在國中小學的數學課堂上,顯然也值得將摺紙數學推薦成為一個有意義的教學活動,這是本書第二篇「摺紙與幾何教學」的主要構想。事實上,如果大家有機會欣賞英國數學家楊氏伉儷檔 (Grace Chisholm Young & W. H. Young) 的百年前經典作 Beginner’s Book of Geometry (1905),一定會同意摺紙學數學原來早就可以登上中小學課堂!在本書中,謝豐瑞教授的〈使幾何教學活潑化〉清楚地指出:她在十七年前,就已經積極呼籲數學教育界重視摺紙與剪紙的價值與意義了。此外,譚克平教授與他的研究生(也是國中現職教師)合作進行的連結摺紙與尺規作圖之教學研究,放在今天的數學教育之現實脈絡中,更足以反映國內教育專家開拓數學教學多元面向的深刻關懷。在本書第二篇中,為了說明我們不只是紙上談兵,我們特別提供國中基測問題的答案。當然,如果這些試題的討論,讓你覺得有一點濃裝豔抹的「考試味道」,不妨好好地檢視一下土地鑑界問題,相信讀者會有意想不到的收穫才是。
有關摺紙與尺規作圖之連結,我們在本書第三篇中,也提供一些歷史反思性 的論述,譬如摺紙 vs. 尺規作圖等問題,俾便說明這種美勞或遊藝活動,如何可以和「較高階的」數學知識活動連結,其中鬆弛尺規作圖要件的意義,也在摺紙數學的價值發揮中得到抒解。因此,我們希望讀者在閱讀本輯文章時,能適時地交互參考第一篇所提供的摺紙經驗,以便深入理解古希臘數學家,如歐幾里得對於尺規(幾何)作圖要件的堅持之歷史意義。此外,本篇所收葉吉海老師的〈正七邊形的「幾何作圖」〉,也非常值得注意,因為「可能與否」乃是數學知識活動的獨特本質之一,這在其他科技知識活動中,幾乎是完全不具備任何意義的。
對於尺規作圖要件這種看似吹毛求疵的堅持,也引伸了非常有趣的數學史上極為著名的「三大作圖題」,它們的故事不僅促進數學的發展,也豐富現代人的數學經驗與想像。基於此,在本書第四篇中,蘇惠玉老師的〈三大作圖題〉是個舊標題下的新書寫,在結合古希臘哲學與文化背景的論述中,本文洋溢著中學教師的教學關懷,非常值得大力推薦。還有,黃俊瑋的〈精確之必要——從歐幾里得到高斯〉一文,深入說明了數學知識活動中,一個極重要的嚴密 vs. 直觀之處境:在摺紙數學的直觀脈絡中,精確與嚴密還是有其必要。他取徑數學史,說明十九歲高斯所完成的第一個不朽貢獻 – 正十七邊形可以尺規作圖的歷史與認知意義。從這個面向切入,劉柏宏教授的〈「摺紙」——沒有算式的數學〉就顯得語重心長,他介紹摺紙數學研究的最新發展,論述它所面臨的處境,並反思這一智性活動所反應的歷史意義。
總之,我們竭誠地歡迎讀者,尤其是美勞與數學教師,一起與我們分享摺紙的趣味與美學。如果讀者因此觸及相關的數學知識活動,深入其中,享受知識獵奇的樂趣,當然更是善莫大焉。我們希望這一本小小的文集只是一個開端,拋磚引玉,至盼我們有機會分享讀者與其他作者的經驗與心得。最後,竭誠歡迎讀者的指正。
目次
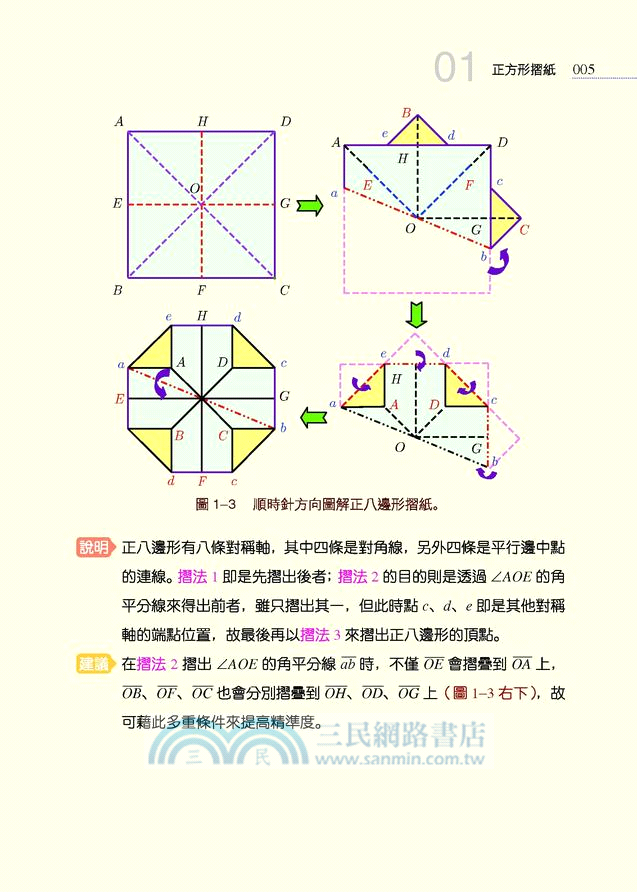
01. 正方形摺紙
02. 正三角形摺紙
03. 五角星形的許願星
04. 正六邊形的平安符
第二篇 摺紙與幾何教學
05. 使幾何教學活潑化 —— 摺紙及剪紙篇
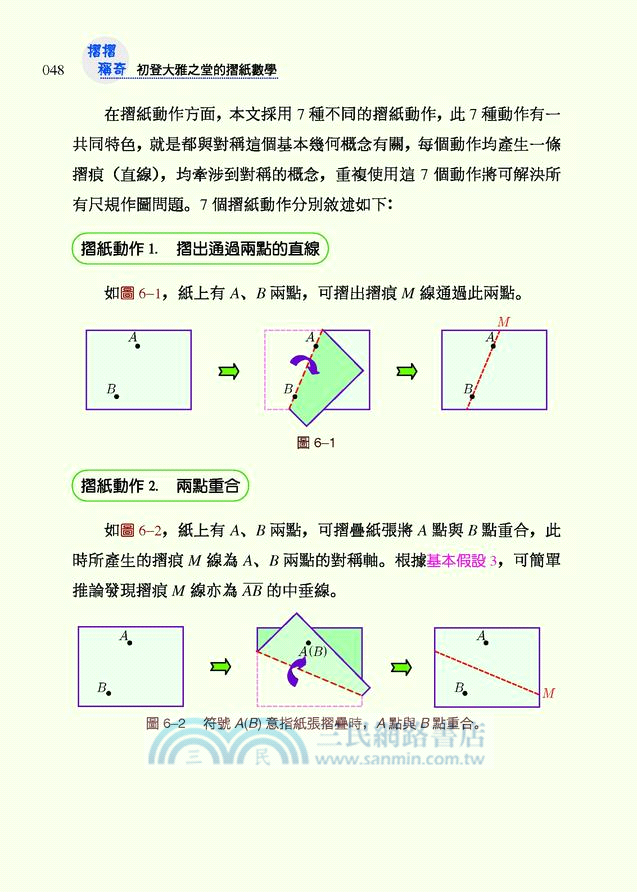
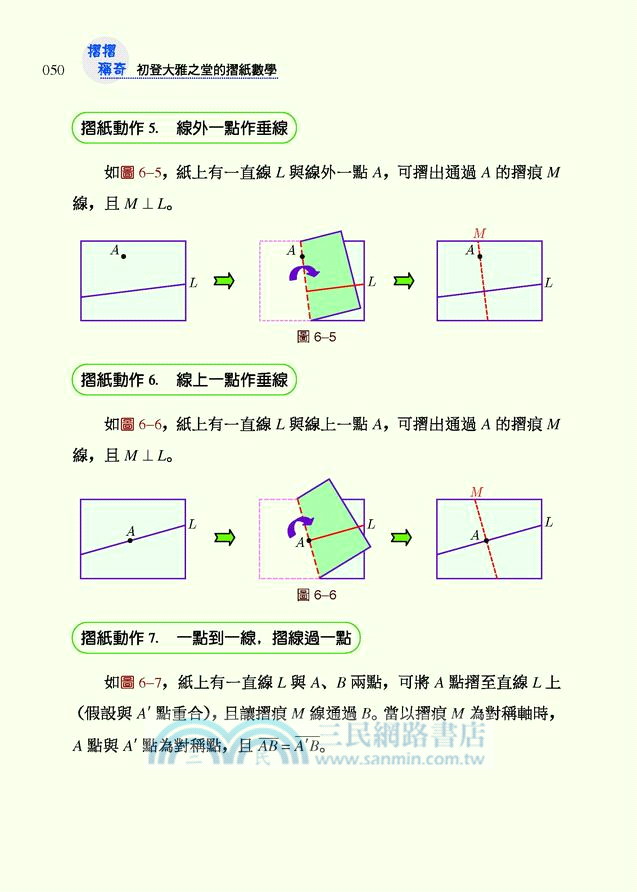
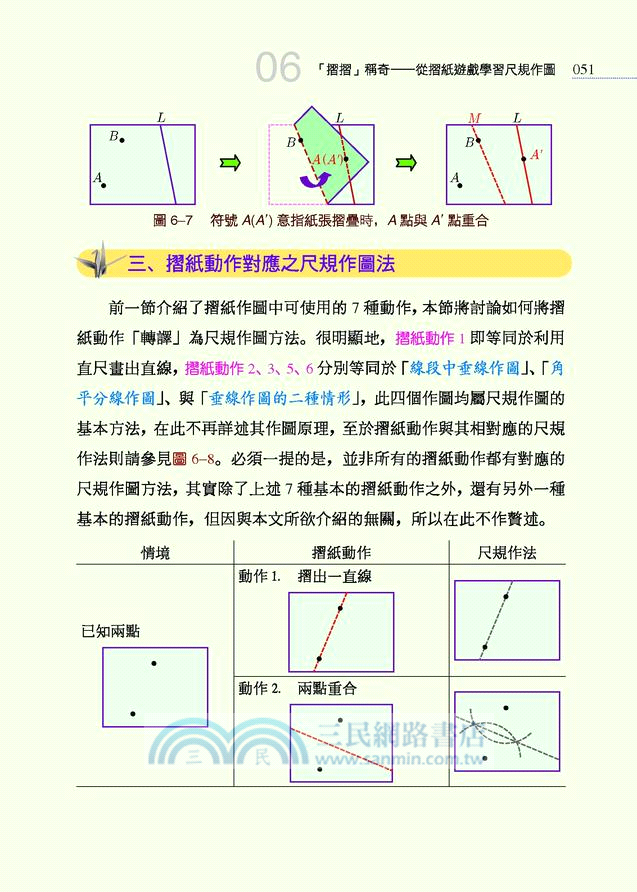
06. 「摺摺」稱奇 —— 從摺紙遊戲學習尺規作圖
07. 運用摺紙提升學生尺規作圖技巧
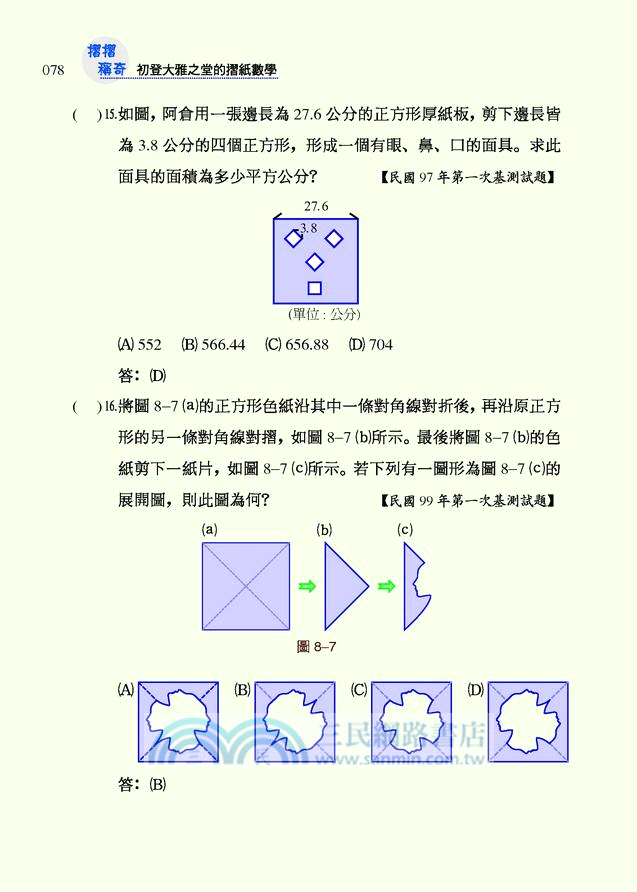
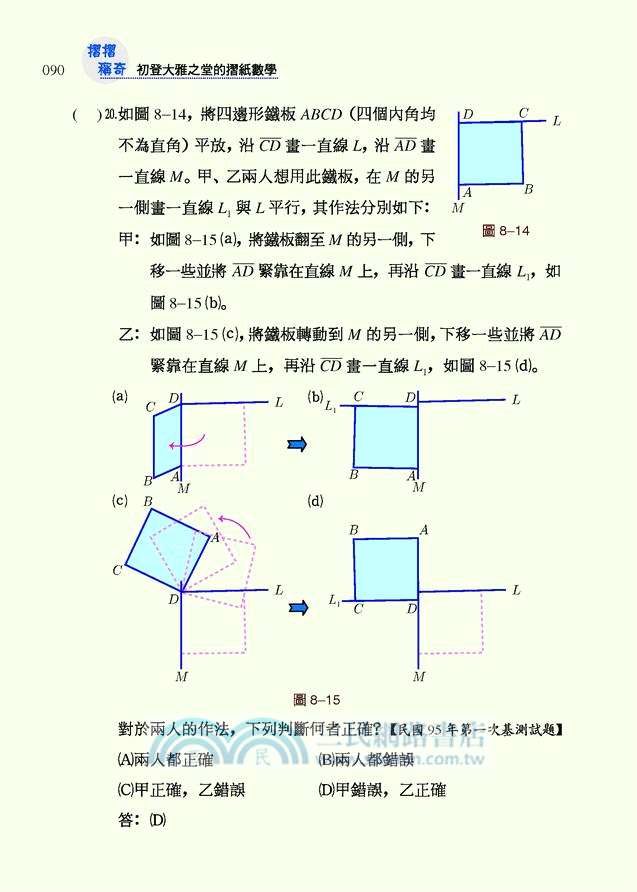
08. 國中基測摺紙與尺規試題彙編
09. 「土地鑑界」問題
第三篇 尺規作圖的意義
10. 尺規作圖 —— 正 3 、 4 、 5 、 6 、 15 邊形
11. 正 7 邊形的「幾何作圖」
12. 幾何作圖 —— 「規矩」 vs. 「規」「矩」
第四篇 精確嚴密數學之必要
13. 三大作圖題
14. 精確之必要 —— 從歐幾里得到高斯
15. 「摺紙」 —— 沒有算式的數學
評論 新增評論
主題書展
更多書展今日66折
您曾經瀏覽過的商品
購物須知
為了保護您的權益,「三民網路書店」提供會員七日商品鑑賞期(收到商品為起始日)。
若要辦理退貨,請在商品鑑賞期內寄回,且商品必須是全新狀態與完整包裝(商品、附件、發票、隨貨贈品等)否則恕不接受退貨。